Example of Coded Inequality in Reasoning
Directions: In the following questions, the symbols δ, @, ©, % and ⋆ are used with the following meaning as illustrated below.
‘A © B’ means ‘A is not smaller than B’.
‘A % B’ means ‘A is neither smaller than nor equal to B ’.
‘A ⋆ B’ means ‘A is neither greater than nor equal to B’.
‘A δ B’ means ‘A is not greater than B’.
‘A @ B’ means ‘A is neither greater than nor smaller than B’.
Now in each of the following questions assuming the given statements to be true, find which of the four conclusions I, II, II and IV given below them is / are definitely true and give your answer accordingly.
Statements:
P δ T, T @ R, R © O, O % K
Conclusions:
I. R @ P
II. R % P
III. K ⋆ T
IV. O δ T
1) Only either I or II is true
2) Only III and IV are true
3) Only either I or II and III are true
4) Only either I or II and IV are true
5) Only either I or II and III and IV are true
Steps Involved in Solving Coded Inequality in Reasoning
Step 1: Make Decoding Table.
The easiest method is to first make a table as shown below.
NOTE: Elements used in question are A and B so we have added A and B in table.
TIP: Sometimes, to make questions more complicated, reverse relations may be given as:
‘A * B’ means ‘B is not smaller than A’.
So here we will write B in the first row and A in the last row.
Step 2: Add Symbols to Table
Step 3: Start decoding symbols one by one. Then add decoded operator into the table.
Here symbols are:
© → not smaller than → means greater than or equal to → ‘≥’
% → neither smaller than nor equal to → means greater than → ‘>’
⋆ → neither greater than nor equal to → means smaller than → ‘<’
δ → not greater than → means smaller than or equal to → ‘≤’
@ → neither greater than nor smaller than → means equal to → ‘=’
So our decoding table becomes:
Step 4: Decode Statements using Decoding Table.
Statements: P δ T, T @ R, R © O, O % K
Decoded statements: P ≤ T, T = R, R ≥ O, O > K
Step 5: Combine Decoded Statements
Combined statement will be: P ≤ T = R ≥ O > K
Step 6: Conclude Individually
Look at conclusions one by one, decode each conclusion using the Decoding Table. Then check whether the conclusion follows or not.
Conclusion I: R @ P → R = P
Now from the combined statement we get, P ≤ T = R.
According to priority level we get, P ≤ R.
Thus R = P is false.
Conclusion II: R % P → R > P
From the combined statement we get, P ≤ T = R.
Thus again we get P ≤ R.
So R > P is false.
But we know from the combined statement that P ≤ R. Hence either conclusion I or II has to be true as they form complementary pair.
Conclusion III: K ⋆ T → K < T
Now from the combined statement we get T = R ≥ O > K.
This can be shortened as T ≥ O > K.
Now according to priority, > has more priority than ≥. So the final relation between T and K will be T > K.
Thus the conclusion is true.
Conclusion IV: O δ T → O ≤ T
Now from the combined statement we get, T = R ≥ O.
According to priority, ≥ has more priority than =. So the final relation between T and O will be T ≥ O.
Thus the conclusion is true.
Now, Try it Yourself
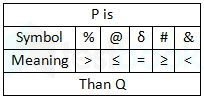
Directions: In the following questions, the symbols δ, @, #, % and & are used with the following meaning as illustrated below.
‘P % Q’ means ‘P is neither smaller than nor equal to Q’.
‘P @ Q’ means ‘P is not greater than Q’.
‘P δ Q’ means ‘P is neither greater than nor smaller than Q’.
‘P # Q’ means ‘P is not smaller than Q’.
‘P & Q’ means ‘P is neither greater than nor equal to Q’.
Now is each of the following questions assuming the given statements to be true, find which of the three conclusions I, II, II and IV given below them is / are definitely true and give your answer accordingly.
Statements:
J δ F, F @ N, N % H, H # G
Conclusions:
I. G & N
II. N # J
III. F & J
IV. J @ G
Solution
From the given statement we get the following table,
 |
| Add caption |
Given statements: J δ F, F @ N, N % H, H # G
Decoded statement: J = F, F ≤ N, N > H, H ≥ G
Combined statement: J = F ≤ N > H ≥ G
Conclusions:
I. G & N → G < N → From statement: N > H ≥ G → N > G → hence true.
II. N # J → N ≥ J → From statement: J = F ≤ N → J ≤ N → hence true.
III. F & J → F < J → From statement: J = F → hence false.
IV. J @ G → J ≤ G → From statement: J = F ≤ N > H ≥ G → J ≤ N > H ≥ G → J ≤ N > G → thus we can say that, clear relationship between J and G cannot be established → hence false.
Hence only conclusion I and II follows.
Comments
Post a Comment